Watt curve: Difference between revisions
From JSXGraph Wiki
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
=Trace= | |||
With JSXGraph elements can be traced to visualize construced loci. | With JSXGraph elements can be traced to visualize construced loci. | ||
| Line 56: | Line 57: | ||
</source> | </source> | ||
=Compute Locus Equation= | |||
One way to compute the locus equation of the traced points in the above construction is the Groebner-Basis-Method. Applying this method to the above construction we get this polynomial: | |||
<math>16e^4s^2 - 96e^3s^3 + 208e^2s^4 - 192es^5 + 64s^6 + 16e^4t^2 - 96e^3st^2 + 288e^2s^2t^2 - 384es^3t^2 + 192s^4t^2 + 80e^2t^4 - 192est^4 + 192s^2t^4 + 64t^6 + 136e^3s - 680e^2s^2 + 1088es^3 - 544s^4 - 1432e^2t^2 + 1088est^2 - 1088s^2t^2 - 544t^4 + 289e^2 - 1156es + 1156s^2 + 1156t^2</math> | |||
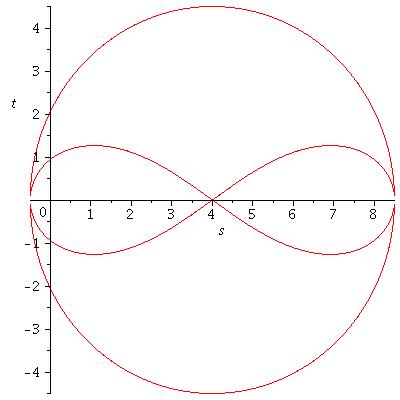
Where in this case <math>e=8</math>. Setting the polynomial to zero and plotting that equation with Maple results the following picture. | |||
[[Image:Plot_watt_curve.jpeg]] | |||
[[Category:Examples]] | [[Category:Examples]] | ||
[[Category:Curves]] | [[Category:Curves]] | ||
Revision as of 09:55, 27 April 2009
Trace
With JSXGraph elements can be traced to visualize construced loci.
References
The underlying JavaScript code
board = JXG.JSXGraph.initBoard('jxgbox', {originX: 50, originY: 400, unitX: 25, unitY: 25, axis: false, grid: false});
xax = board.createElement('axis', [[0,0],[1,0]]);
yax = board.createElement('axis', [[0,0],[0,1]]);
p1 = board.createElement('point', [7, 8], {style:2,name:"",fixed:true});
p2 = board.createElement('point', [15, 8], {style:2,name:"",fixed:true});
c1 = board.createElement('circle', [p1, 4.5]);
c2 = board.createElement('circle', [p2, 4.5]);
g1 = board.createElement('glider', [0, 0, c1], {style:5,name:"Drag me"});
c3 = board.createElement('circle', [g1, 8]);
g2 = board.createElement('point', [board.intersectionFunc(c2,c3,0)], {style:5, name: ""});
g3 = board.createElement('point', [board.intersectionFunc(c2,c3,1)], {style:5, name: ""});
m1 = board.createElement('midpoint', [g1,g2], {style:8,name:"",trace:true});
m2 = board.createElement('midpoint', [g1,g3], {style:8,name:"",trace:true,strokeColor:'green'});
function clearTrace() {
m1.clearTrace();
m2.clearTrace();
}
Compute Locus Equation
One way to compute the locus equation of the traced points in the above construction is the Groebner-Basis-Method. Applying this method to the above construction we get this polynomial:
[math]\displaystyle{ 16e^4s^2 - 96e^3s^3 + 208e^2s^4 - 192es^5 + 64s^6 + 16e^4t^2 - 96e^3st^2 + 288e^2s^2t^2 - 384es^3t^2 + 192s^4t^2 + 80e^2t^4 - 192est^4 + 192s^2t^4 + 64t^6 + 136e^3s - 680e^2s^2 + 1088es^3 - 544s^4 - 1432e^2t^2 + 1088est^2 - 1088s^2t^2 - 544t^4 + 289e^2 - 1156es + 1156s^2 + 1156t^2 }[/math]
Where in this case [math]\displaystyle{ e=8 }[/math]. Setting the polynomial to zero and plotting that equation with Maple results the following picture.