Watt curve
From JSXGraph Wiki
Trace
With JSXGraph elements can be traced to visualize construced loci.
References
The underlying JavaScript code
board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 16, 22, -2], axis: true, grid: false});
p1 = board.create('point', [7, 8], {face:'x',size:4,name:"",fixed:true});
p2 = board.create('point', [15, 8], {face:'x',size:4,name:"",fixed:true});
c1 = board.create('circle', [p1, 4.5]);
c2 = board.create('circle', [p2, 4.5]);
g1 = board.create('glider', [0, 0, c1], {size:3,name:"Drag me"});
c3 = board.create('circle', [g1, 8]);
g2 = board.create('point', [board.intersectionFunc(c2,c3,0)], {size:3, name: ""});
g3 = board.create('point', [board.intersectionFunc(c2,c3,1)], {size:3, name: ""});
m1 = board.create('midpoint', [g1,g2], {face:'[]',size:3,withLabel:false,trace:true});
m2 = board.create('midpoint', [g1,g3], {face:'[]',size:3,withLabel:false,trace:true,strokeColor:'green'});
function clearTrace() {
m1.clearTrace();
m2.clearTrace();
}
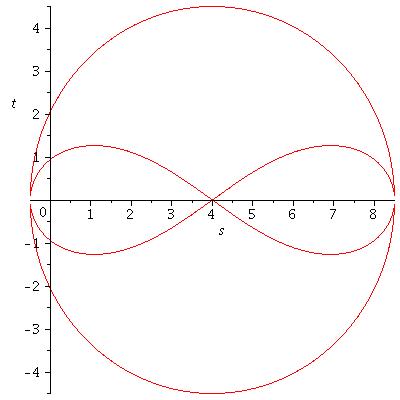
Compute Locus Equation
One way to compute the locus equation of the traced points in the above construction is the Groebner-Basis-Method. Applying this method to the above construction we get this polynomial:
[math]\displaystyle{ 16e^4s^2 - 96e^3s^3 + 208e^2s^4 - 192es^5 + 64s^6 + 16e^4t^2 - 96e^3st^2 + 288e^2s^2t^2 - 384es^3t^2 + 192s^4t^2 + 80e^2t^4 - 192est^4 + 192s^2t^4 + 64t^6 + 136e^3s - 680e^2s^2 + 1088es^3 - 544s^4 - 1432e^2t^2 + 1088est^2 - 1088s^2t^2 - 544t^4 + 289e^2 - 1156es + 1156s^2 + 1156t^2 }[/math]
Where in this case [math]\displaystyle{ e=8 }[/math]. Setting the polynomial to zero and plotting that equation with Maple results the following picture.